图（上）

Posted on   |   In   |  

一.什么是图

1.基本定义

  • 表示“多对多”的一种关系，树是一对多，线性结构是一对一，可以看作图的特殊情况。
    包含：
    • 一组顶点（通常用V(Vertex)表示顶点集合
    • 一组边：通常用E（Edge）表示边的集合
      • 边是顶点对：（v，w）属于E，其中v，w属于V，
      • 有向边：<v, w> 表示v指向w的边 （单行线）
        注意：一对圆括号表示双向边，一对尖括号表示单向边
        图中没有重复边（两个顶点之间，当边是无向边时，默认只有一条边，不会有多条边）和自回路（顶点不会指向自身）
    • 图可以没有边，但是不能没有顶点
    • 无向图：边没有方向
    • 有向图：边有方向（双向，单向，边可能带权重）

2.在程序中如何表示图

  • 邻接矩阵
    • 邻接矩阵G[N][N] —- N个顶点从0到N-1编号
    • G[i][j] = 1,表示Vi到Vj的边， G[i][j] = 0，表示Vi和Vj之间没有直接相连的边
    • 如果是无向图，则其邻接矩阵是关于对角线对称的，切对角线的元素均为0，因为图没有自回路，具体可见MOOC6.1第二个小视频。
    • 由上面可知，这样存储会浪费一半空间，如何节省空间，使用一个长度为N（N+1)/2的一维数组来存储，只存储下三角矩阵的元素，Gij在一维数组A中对应的下标应该是i*(i+1)/2 +j,视情况而定，对于有权值的图，则可以将矩阵中对应位置元素的值记为权重，如果没有权重，则记为1，代表两点之间有边，记为0，代表两点直接没有直接边相连。
    • 邻接矩阵的好处：
      • 方便查找任一顶点的所有邻接点（有直接边相连的顶点）–遍历矩阵的某一行元素，元素为1，则直接相连
      • 方便计算任一顶点的“度”（从该点出发的边数为“出度”，指向该点的边数为“入度”）
        • 无向图：对应行（列）非0元素的个数
        • 有向图：对应行非0元素的个数是“出度”，对应列非0元素的个数是“入度”
    • 邻接矩阵的缺点：
      • 对于存稀疏图，会浪费空间（对于稠密图，尤其是完全图（任一两点直接相连），还是挺合算的）
      • 浪费时间（统计稀疏图有多少条边的时候）
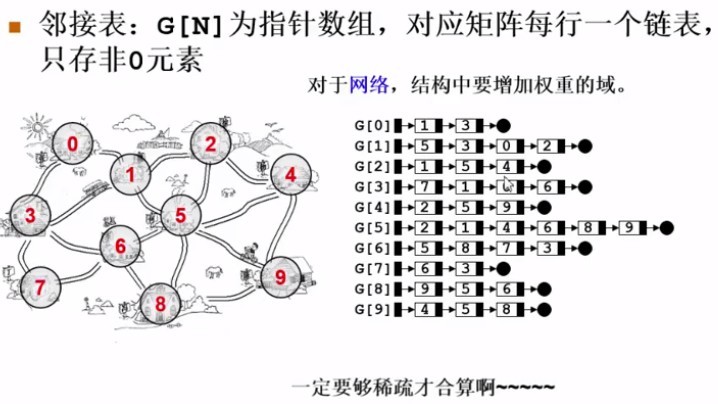
  • 邻接表
    • Alt text
    • 邻接表的优点：
      • 方便找任一节点的邻接点
      • 节约稀疏图的空间（需要N个头指针+2E个结点（每个结点至少两个域））问：E小于多少，用邻接表划算： N + 2E2 < N*N 解得：E< N(N-1)/4;
      • 方便计算任一节点的”度”？
        • 对于无向图 ，是的
        • 对有向图，只能计算出度，需要计算“逆邻接表”（存指向自己的边）来方便计算“入度”
      • 不方便计算任一两点之间是否存在边

二.图的遍历

1.深度优先搜索（Depth First Search， DFS）

  • 伪码描述
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    void DFS(Vertex V)
    {
    	visited[V] = true;//代表该结点被访问了
    	for(V的每个邻接点W)
    	{
    		if(!visited[W])	//如果还没被访问过
    		{
    			DFS(W);
    		}
    	}
    }

跟树的先序遍历很类似

  • 时间复杂度
    若有N个顶点，E条边，时间复杂度是
    • 若用邻接表存储图，有O(N+E); //邻接表只要遍历N个结点后面的链接的个数E即可
    • 若邻接矩阵存储图，有O(N^2); //邻接矩阵需要遍历N个结点后面的链接的个数N

2.广度优先搜索（Breadth First Search，BFS）

  • 伪代码
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    void BFS(Vertex V)
    {
    	visited[V] = true;
    	EnQuene(V,Q);//入队
    	while(!IsEmpty(Q))
    	{
    		V = DeQuene(Q);//出队
    		for(V的每个邻接点W)
    		{
    			if(!visited[W])
    			{
    				visited[W] = true;
    				EnQuene(W, Q);
    			}
    		}
    	}

    }
跟树的层次遍历很类似
  • 时间复杂度
    和DFS一样

3.名词解释：

  • 概念

    • 连通：如果V到W存在一条路径，则称V和W是连通的
    • 路径：V和W的路径是一系列顶点｛V，V1，V2···｝的集合，其中任一对相邻顶点都是图中的边。路径的长度是路径中的边数（如果带权，则是所有边的权重和），如果V到W之间的所有顶点都不同，则称简单路径。
    • 回路：起点等于终点的路径
    • 连通分量（指的是无向图）：无向图的极大连通子图
      • 极大定点数：再加一个顶点就不连通了（加的这个顶点要属于这个图）
      • 极大边数：包含子图中所有顶点相连的所有边
    • 强连通：有向图中顶点V和W之间存在双向路径，则称V和W是强连通的
    • 弱连通：有向图中顶点V和W之间不存在双向路径，但是去掉方向，就是连通的，则称V和W是弱连通的
    • 强连通图：有向图中任一两顶点均强连通
    • 强连通分量：有向图的极大强连通子图

  • 图不连通怎么办？（如何遍历？）

    • 伪码描述
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      void ListCompontents(Graph G)
      {
      	for(each V in G)
      	{
      		if(!visited[V])
      		{
      			DFS(V);	//or BFS(V);	//每一个DFS(BFS)遍历一个连通分量
      		}
      	}
      }